引言

圆锥曲线是数学中一个重要的研究领域，它在几何、物理和工程等领域都有着广泛的应用。圆锥曲线齐次式是圆锥曲线的一个重要特性，它将圆锥曲线的方程表示为齐次形式，使得研究变得更加简洁和统一。本文将围绕圆锥曲线齐次式展开，探讨其基本性质、应用以及解法。

圆锥曲线齐次式的定义

圆锥曲线齐次式是指将圆锥曲线的方程通过适当的变换，使其成为齐次方程的一种形式。具体来说，对于任意一个圆锥曲线，我们可以通过坐标变换，将其方程表示为以下形式：

[ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 ] 其中，A、B、C、D、E、F是实数，且A、B、C不全为零。

圆锥曲线齐次式的性质

圆锥曲线齐次式具有以下性质：

• 齐次性：齐次式的系数与坐标的比例无关，这意味着曲线的形状和位置不随坐标比例的变化而改变。

• 对称性：齐次式在坐标轴上的对称性保证了曲线在坐标轴上的对称性。

• 不变性：齐次式在坐标变换下保持不变，这使得我们可以通过坐标变换来研究圆锥曲线的性质。

圆锥曲线齐次式的应用

圆锥曲线齐次式在数学和实际应用中都有着广泛的应用，以下是一些例子：

• 几何学：通过圆锥曲线齐次式，我们可以研究圆锥曲线的对称性、交点、切线等性质。

• 物理学：在光学中，圆锥曲线齐次式被用来描述光线的传播路径，如抛物线、双曲线和椭圆等。

• 工程学：在工程设计中，圆锥曲线齐次式可以用来分析物体的运动轨迹，如卫星轨道、火箭轨迹等。

圆锥曲线齐次式的解法

解圆锥曲线齐次式通常涉及以下步骤：

1. 将齐次式转换为标准形式：通过适当的坐标变换，将齐次式转换为标准形式，如椭圆、双曲线或抛物线的标准方程。

2. 求解参数方程：将标准形式的方程转换为参数方程，以便于分析和绘图。

   

3. 研究性质：根据参数方程，研究圆锥曲线的几何性质，如焦点、准线、渐近线等。

实例分析

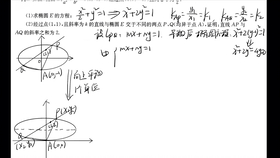
以下是一个具体的例子，我们将通过圆锥曲线齐次式来分析一个椭圆的性质。

给定椭圆的方程为：

[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 ] 其中，a和b是椭圆的半长轴和半短轴。

通过坐标变换，我们可以将上述方程转换为齐次式：

[ \frac{x^2}{a^2} + \frac{y^2}{b^2} - 1 = 0 ] 这个齐次式具有以下性质：

• 对称性：椭圆关于x轴和y轴都是对称的。

• 不变性：椭圆的形状和位置不随坐标比例的变化而改变。

通过参数方程，我们可以进一步研究椭圆的几何性质，如焦点、准线等。

结论

圆锥曲线齐次式是研究圆锥曲线的一个重要工具，它不仅简化了方程的形式，而且使得圆锥曲线的性质研究变得更加统一和系统。通过对圆锥曲线齐次式的深入理解和应用，我们可以更好地掌握圆锥曲线的几何和物理性质，为数学和实际应用提供有力的支持。